Inversely Proportional on:
[Wikipedia]
[Google]
[Amazon]

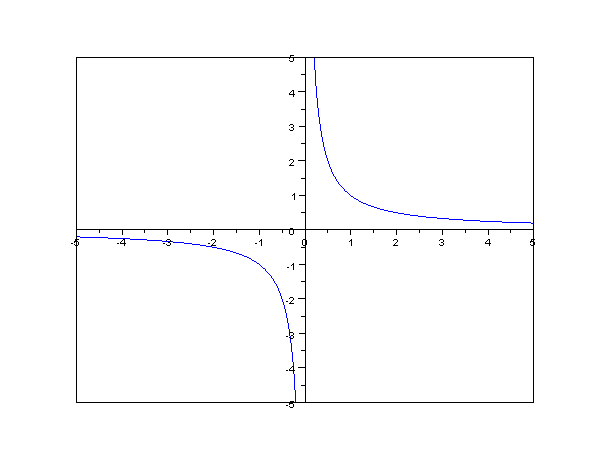 In
In
 The concept of ''inverse proportionality'' can be contrasted with ''direct proportionality''. Consider two variables said to be "inversely proportional" to each other. If all other variables are held constant, the magnitude or absolute value of one inversely proportional variable decreases if the other variable increases, while their product (the constant of proportionality ''k'') is always the same. As an example, the time taken for a journey is inversely proportional to the speed of travel.
Formally, two variables are inversely proportional (also called varying inversely, in inverse variation, in inverse proportion) if each of the variables is directly proportional to the multiplicative inverse (reciprocal) of the other, or equivalently if their product is a constant.Weisstein, Eric W
The concept of ''inverse proportionality'' can be contrasted with ''direct proportionality''. Consider two variables said to be "inversely proportional" to each other. If all other variables are held constant, the magnitude or absolute value of one inversely proportional variable decreases if the other variable increases, while their product (the constant of proportionality ''k'') is always the same. As an example, the time taken for a journey is inversely proportional to the speed of travel.
Formally, two variables are inversely proportional (also called varying inversely, in inverse variation, in inverse proportion) if each of the variables is directly proportional to the multiplicative inverse (reciprocal) of the other, or equivalently if their product is a constant.Weisstein, Eric W
"Inversely Proportional"
''MathWorld'' – A Wolfram Web Resource. It follows that the variable ''y'' is inversely proportional to the variable ''x'' if there exists a non-zero constant ''k'' such that : or equivalently, Hence the constant "''k''" is the product of ''x'' and ''y''. The graph of two variables varying inversely on the Cartesian coordinate plane is a rectangular hyperbola. The product of the ''x'' and ''y'' values of each point on the curve equals the constant of proportionality (''k''). Since neither ''x'' nor ''y'' can equal zero (because ''k'' is non-zero), the graph never crosses either axis.
p. 34–35
* Brian Burrell: ''Merriam-Webster's Guide to Everyday Math: A Home and Business Reference''. Merriam-Webster, 1998,
p. 85–101
* Lanius, Cynthia S.; Williams Susan E.
''PROPORTIONALITY: A Unifying Theme for the Middle Grades''
Mathematics Teaching in the Middle School 8.8 (2003), p. 392–396. * Seeley, Cathy; Schielack Jane F.
''A Look at the Development of Ratios, Rates, and Proportionality''
Mathematics Teaching in the Middle School, 13.3, 2007, p. 140–142. * Van Dooren, Wim; De Bock Dirk; Evers Marleen; Verschaffel Lieven
''Students' Overuse of Proportionality on Missing-Value Problems: How Numbers May Change Solutions''
Journal for Research in Mathematics Education, 40.2, 2009, p. 187–211. {{DEFAULTSORT:Proportionality (Mathematics) Mathematical terminology Ratios
 In
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio, which is called the coefficient of proportionality or proportionality constant. Two sequences are inversely proportional if corresponding elements have a constant product, also called the coefficient of proportionality.
This definition is commonly extended to related varying quantities, which are often called ''variables''. This meaning of ''variable'' is not the common meaning of the term in mathematics (see variable (mathematics)); these two different concepts share the same name for historical reasons.
Two functions and are ''proportional'' if their ratio is a constant function
In mathematics, a constant function is a function whose (output) value is the same for every input value. For example, the function is a constant function because the value of is 4 regardless of the input value (see image).
Basic properties ...
.
If several pairs of variables share the same direct proportionality constant, the equation
In mathematics, an equation is a formula that expresses the equality of two expressions, by connecting them with the equals sign . The word ''equation'' and its cognates in other languages may have subtly different meanings; for example, in ...
expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio).
Proportionality is closely related to '' linearity''.
Direct proportionality
Given two variables ''x'' and ''y'', ''y'' is directly proportional to ''x'' if there is a non-zero constant ''k'' such that : The relation is often denoted using the symbols "∝" (not to be confused with the Greek letteralpha
Alpha (uppercase , lowercase ; grc, ἄλφα, ''álpha'', or ell, άλφα, álfa) is the first letter of the Greek alphabet. In the system of Greek numerals, it has a value of one. Alpha is derived from the Phoenician letter aleph , whic ...
) or "~":
: or
For the proportionality constant can be expressed as the ratio
:
It is also called the constant of variation or constant of proportionality.
A direct proportionality can also be viewed as a linear equation
In mathematics, a linear equation is an equation that may be put in the form
a_1x_1+\ldots+a_nx_n+b=0, where x_1,\ldots,x_n are the variables (or unknowns), and b,a_1,\ldots,a_n are the coefficients, which are often real numbers. The coefficien ...
in two variables with a ''y''-intercept of and a slope of ''k''. This corresponds to linear growth.
Examples
* If an object travels at a constant speed, then the distance traveled is directly proportional to the time spent traveling, with the speed being the constant of proportionality. * The circumference of a circle is directly proportional to its diameter, with the constant of proportionality equal to . * On a map of a sufficiently small geographical area, drawn toscale
Scale or scales may refer to:
Mathematics
* Scale (descriptive set theory), an object defined on a set of points
* Scale (ratio), the ratio of a linear dimension of a model to the corresponding dimension of the original
* Scale factor, a number ...
distances, the distance between any two points on the map is directly proportional to the beeline distance between the two locations represented by those points; the constant of proportionality is the scale of the map.
* The force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a p ...
, acting on a small object with small mass by a nearby large extended mass due to gravity, is directly proportional to the object's mass; the constant of proportionality between the force and the mass is known as gravitational acceleration.
* The net force acting on an object is proportional to the acceleration of that object with respect to an inertial frame of reference. The constant of proportionality in this, Newton's second law, is the classical mass of the object.
Computer encoding
Inverse proportionality
 The concept of ''inverse proportionality'' can be contrasted with ''direct proportionality''. Consider two variables said to be "inversely proportional" to each other. If all other variables are held constant, the magnitude or absolute value of one inversely proportional variable decreases if the other variable increases, while their product (the constant of proportionality ''k'') is always the same. As an example, the time taken for a journey is inversely proportional to the speed of travel.
Formally, two variables are inversely proportional (also called varying inversely, in inverse variation, in inverse proportion) if each of the variables is directly proportional to the multiplicative inverse (reciprocal) of the other, or equivalently if their product is a constant.Weisstein, Eric W
The concept of ''inverse proportionality'' can be contrasted with ''direct proportionality''. Consider two variables said to be "inversely proportional" to each other. If all other variables are held constant, the magnitude or absolute value of one inversely proportional variable decreases if the other variable increases, while their product (the constant of proportionality ''k'') is always the same. As an example, the time taken for a journey is inversely proportional to the speed of travel.
Formally, two variables are inversely proportional (also called varying inversely, in inverse variation, in inverse proportion) if each of the variables is directly proportional to the multiplicative inverse (reciprocal) of the other, or equivalently if their product is a constant.Weisstein, Eric W"Inversely Proportional"
''MathWorld'' – A Wolfram Web Resource. It follows that the variable ''y'' is inversely proportional to the variable ''x'' if there exists a non-zero constant ''k'' such that : or equivalently, Hence the constant "''k''" is the product of ''x'' and ''y''. The graph of two variables varying inversely on the Cartesian coordinate plane is a rectangular hyperbola. The product of the ''x'' and ''y'' values of each point on the curve equals the constant of proportionality (''k''). Since neither ''x'' nor ''y'' can equal zero (because ''k'' is non-zero), the graph never crosses either axis.
Hyperbolic coordinates
The concepts of ''direct'' and ''inverse'' proportion lead to the location of points in the Cartesian plane by hyperbolic coordinates; the two coordinates correspond to the constant of direct proportionality that specifies a point as being on a particularray
Ray may refer to:
Fish
* Ray (fish), any cartilaginous fish of the superorder Batoidea
* Ray (fish fin anatomy), a bony or horny spine on a fin
Science and mathematics
* Ray (geometry), half of a line proceeding from an initial point
* Ray (g ...
and the constant of inverse proportionality that specifies a point as being on a particular hyperbola.
See also
* Linear map *Correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics ...
* Eudoxus of Cnidus
Eudoxus of Cnidus (; grc, Εὔδοξος ὁ Κνίδιος, ''Eúdoxos ho Knídios''; ) was an ancient Greek astronomer, mathematician, scholar, and student of Archytas and Plato. All of his original works are lost, though some fragments are ...
* Golden ratio
* Inverse-square law
In science, an inverse-square law is any scientific law stating that a specified physical quantity is inversely proportional to the square of the distance from the source of that physical quantity. The fundamental cause for this can be understo ...
* Proportional font
* Ratio
* Rule of three (mathematics)
* Sample size
* Similarity
* Basic proportionality theorem
The intercept theorem, also known as Thales's theorem, basic proportionality theorem or side splitter theorem is an important theorem in elementary geometry about the ratios of various line segments that are created if two intersecting lines are ...
* ∷ the ''a'' is to ''b'' as ''c'' is to ''d'' symbol (U+2237 ''PROPORTION'')Growth
* Linear growth * Hyperbolic growthNotes
References
* Ya. B. Zeldovich,I. M. Yaglom
Isaak Moiseevich Yaglom (russian: Исаа́к Моисе́евич Ягло́м; 6 March 1921 – 17 April 1988) was a Soviet mathematician and author of popular mathematics books, some with his twin Akiva Yaglom.
Yaglom received a Ph.D. from M ...
: ''Higher math for beginners''p. 34–35
* Brian Burrell: ''Merriam-Webster's Guide to Everyday Math: A Home and Business Reference''. Merriam-Webster, 1998,
p. 85–101
* Lanius, Cynthia S.; Williams Susan E.
''PROPORTIONALITY: A Unifying Theme for the Middle Grades''
Mathematics Teaching in the Middle School 8.8 (2003), p. 392–396. * Seeley, Cathy; Schielack Jane F.
''A Look at the Development of Ratios, Rates, and Proportionality''
Mathematics Teaching in the Middle School, 13.3, 2007, p. 140–142. * Van Dooren, Wim; De Bock Dirk; Evers Marleen; Verschaffel Lieven
''Students' Overuse of Proportionality on Missing-Value Problems: How Numbers May Change Solutions''
Journal for Research in Mathematics Education, 40.2, 2009, p. 187–211. {{DEFAULTSORT:Proportionality (Mathematics) Mathematical terminology Ratios